32 FREE Pythagorean Theorem Worksheets

The Pythagorean Theorem is a mathematical principle that states that in a right-angled triangle, the sum of the squares of two of the shorter sides is equal to the square of the longest side (hypotenuse). The two short sides can be identified as the triangle’s base and perpendicular. 

Its mathematical form is expressed as:

hypotenuse² = perpendicular² + base²,

illustrated as,

c² =a² + b².

By using this formula, we can determine; if a triangle is right-angled, the length of one side of a right-angled triangle provided we know the length of the other sides and the diagonal of a square or rectangle.

This formula has been combined with trigonometry and the six trigonometric ratios: sine, cosine, tangent, secant, cosecant, and cotangent to develop trigonometric functions, which are widely used in various industries.

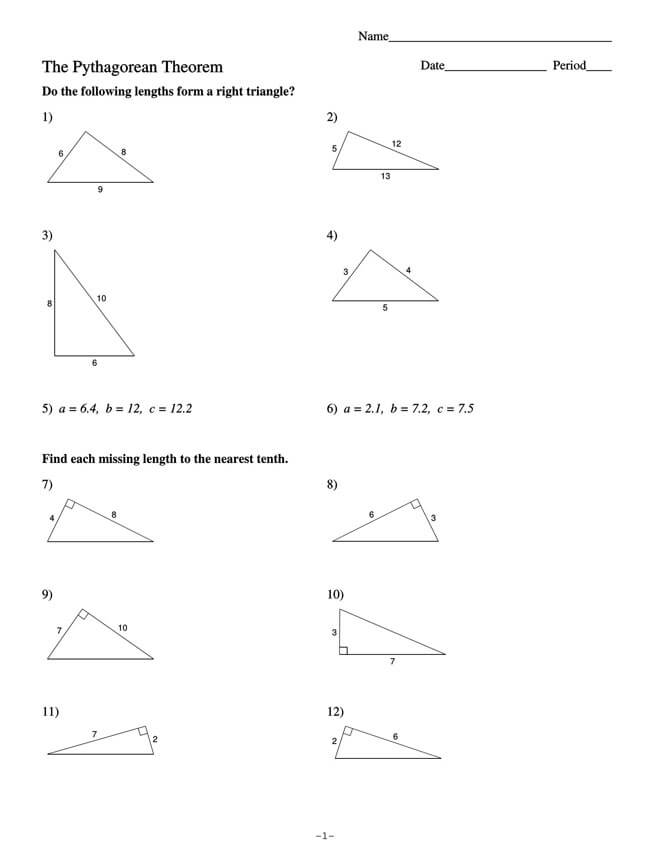
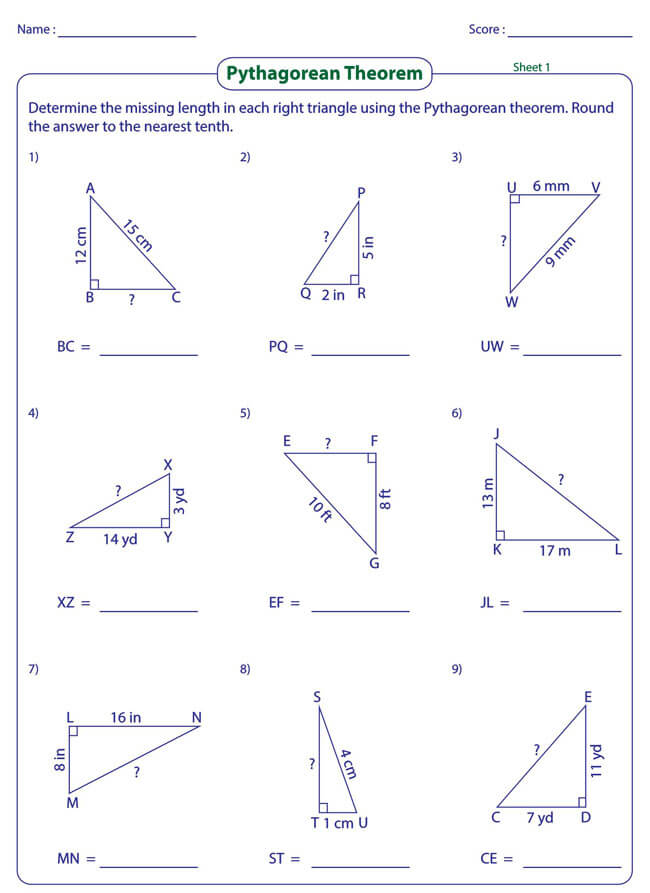
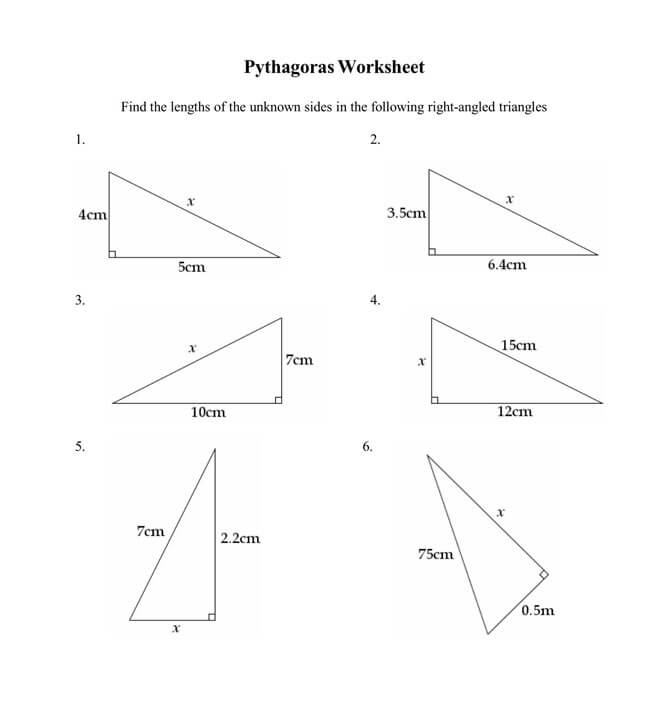
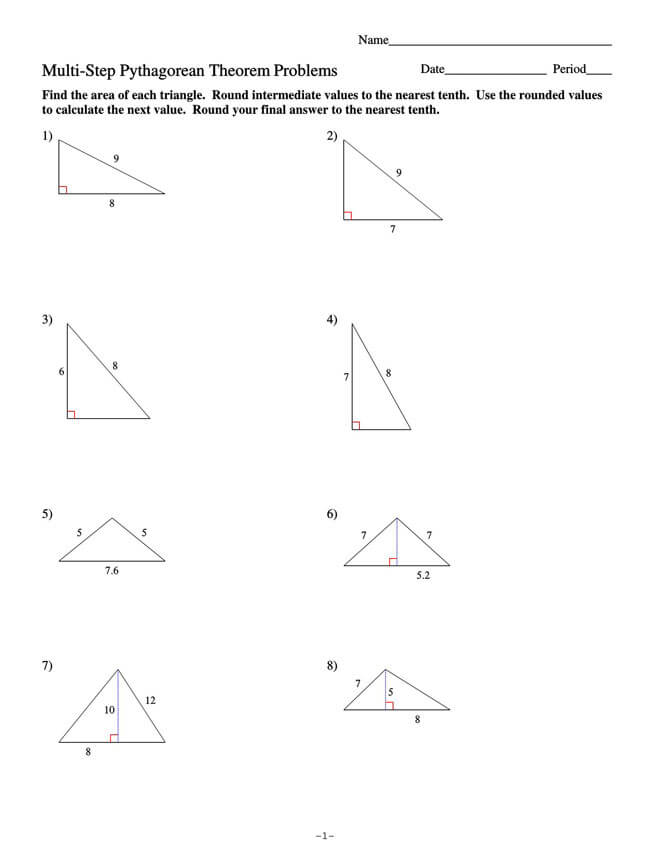
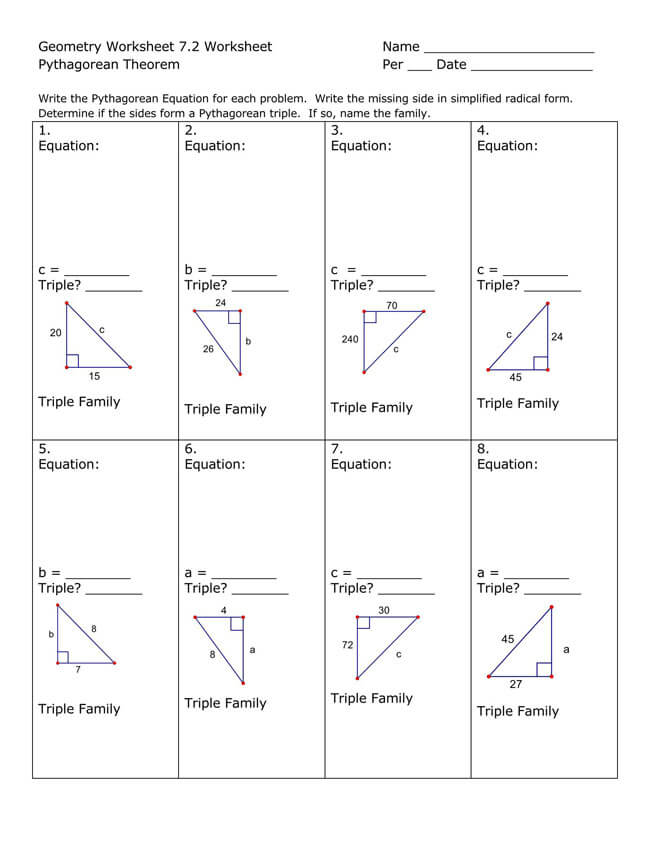
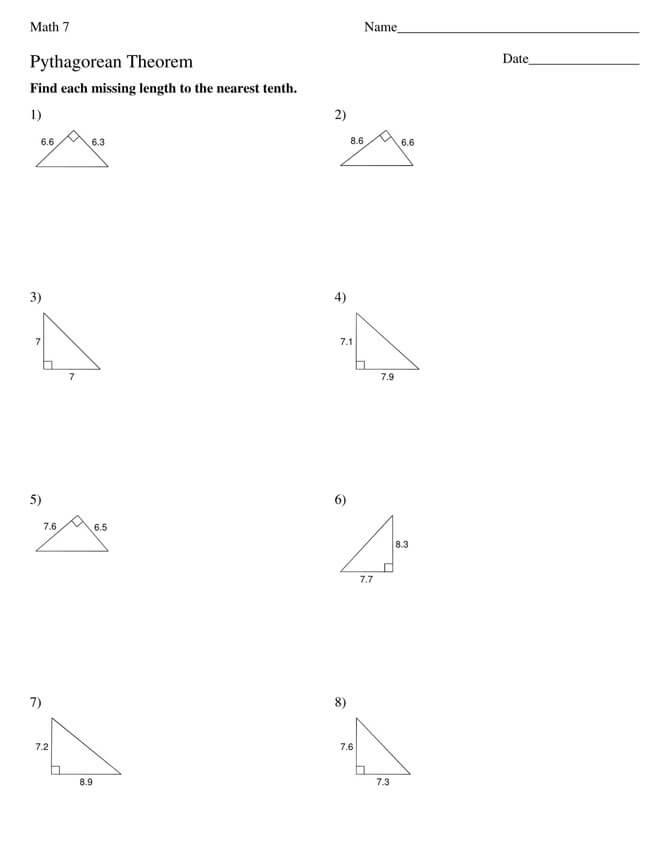
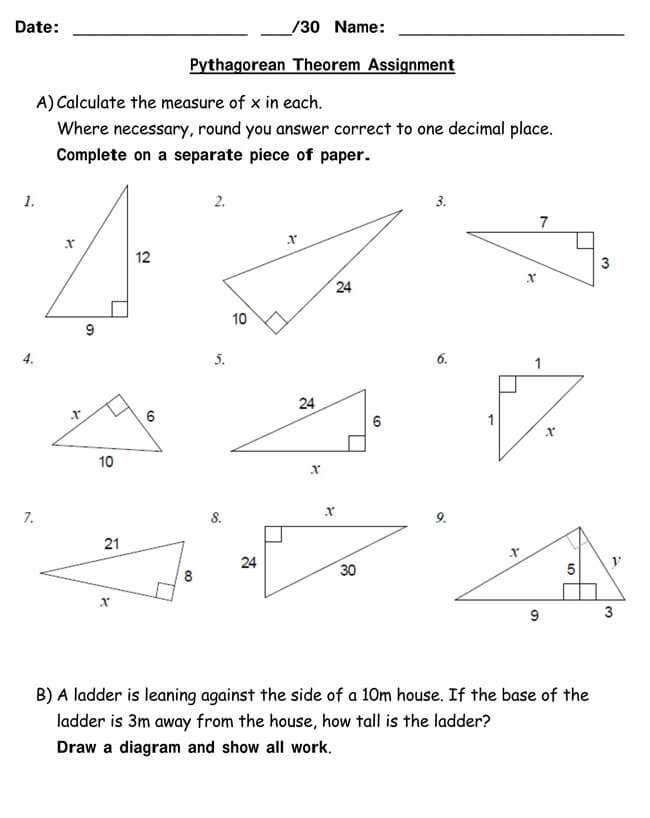
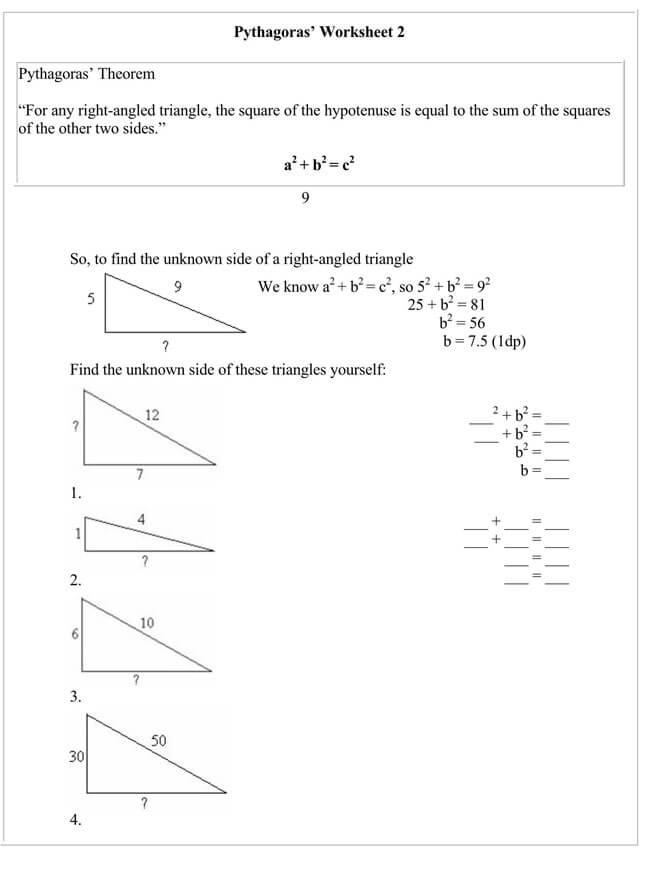
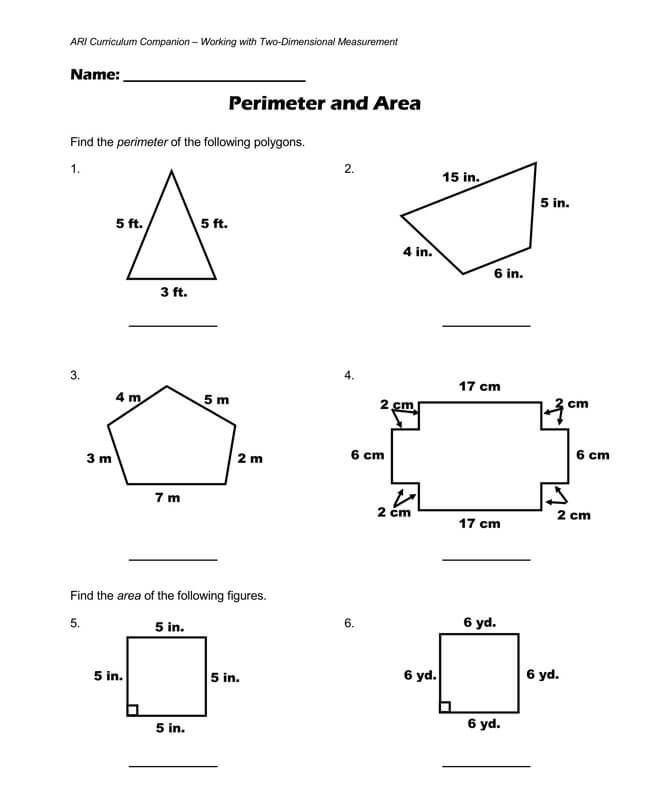
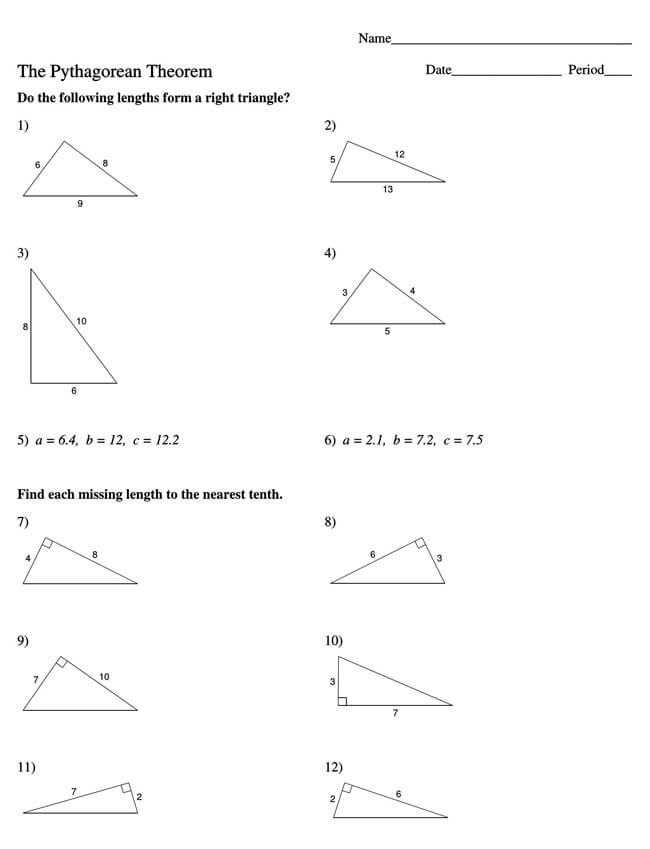
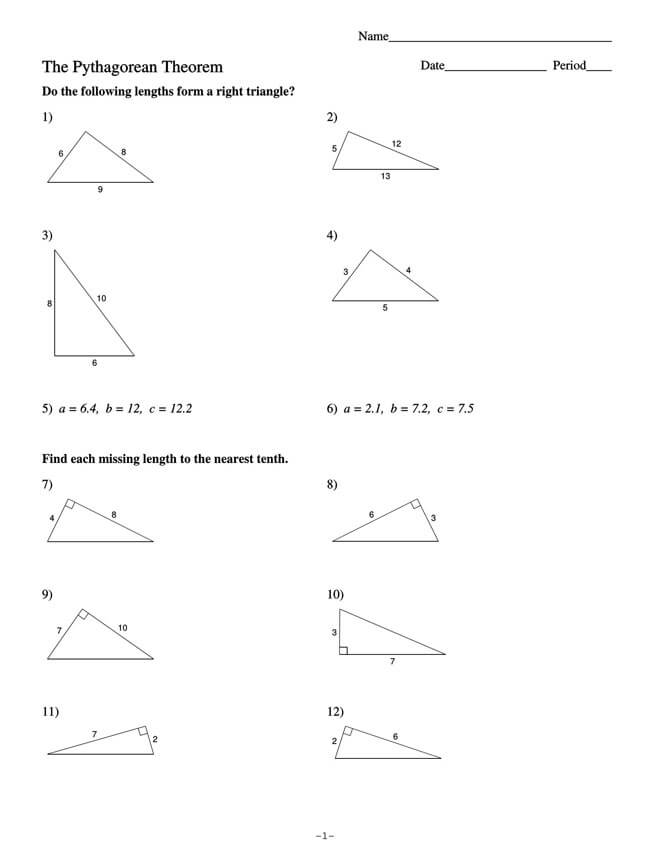
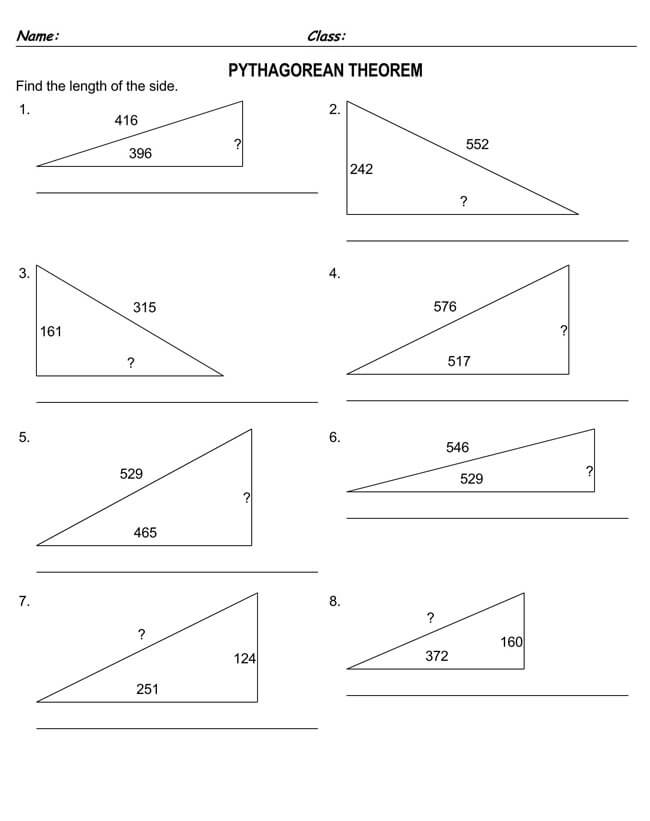
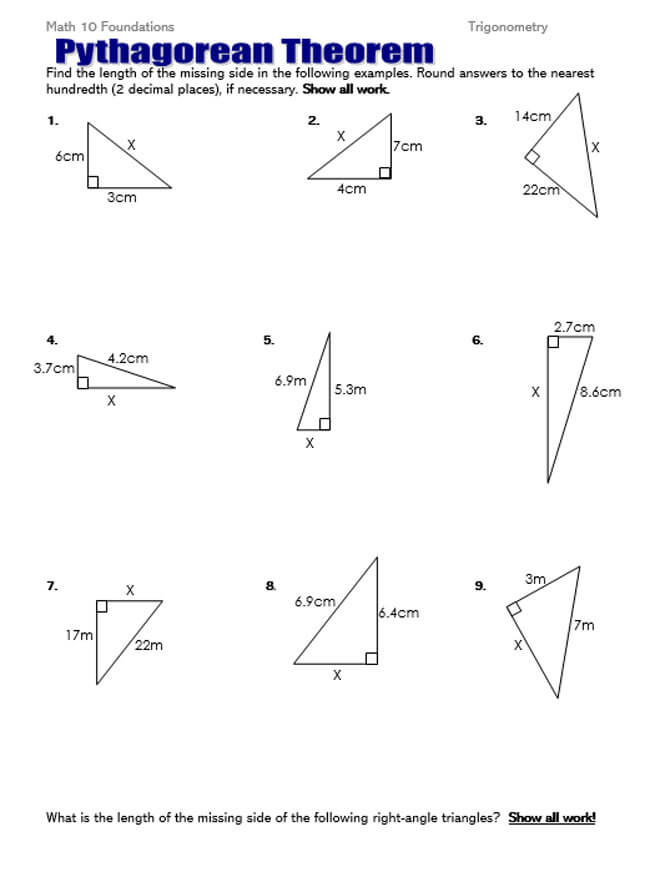
Free Pythagorean Theorem Worksheets

Utilizing the Pythagorean Theorem will often require some mathematical skills, but even if mathematics is not one of your strongest subjects, you can opt to use a worksheet. That is why we have provided you with free Pythagorean Theorem worksheets that you can download and implement in your work.

Pythagorean Theorem Worksheet 01

Pythagorean Theorem Worksheet 02

Pythagorean Theorem Worksheet 03

Pythagorean Theorem Worksheet 04

Pythagorean Theorem Worksheet 05

Pythagorean Theorem Worksheet 06

Pythagorean Theorem Worksheet 07

Pythagorean Theorem Worksheet 08

Pythagorean Theorem Worksheet 09

Pythagorean Theorem Worksheet 10

Pythagorean Theorem Worksheet 11

Pythagorean Theorem Worksheet 12

Pythagorean Theorem Worksheet 13

Pythagorean Theorem Worksheet 14

Pythagorean Theorem Worksheet 15

Pythagorean Theorem Worksheet 16

Pythagorean Theorem Worksheet 17

Pythagorean Theorem Worksheet 18

Pythagorean Theorem Worksheet 19

Pythagorean Theorem Worksheet 20

Pythagorean Theorem Worksheet 21

Pythagorean Theorem Worksheet 22

Pythagorean Theorem Worksheet 23

Pythagorean Theorem Worksheet 24

Pythagorean Theorem Worksheet 25

Pythagorean Theorem Worksheet 26

Pythagorean Theorem Worksheet 27

Pythagorean Theorem Worksheet 28

Pythagorean Theorem Worksheet 29

Pythagorean Theorem Worksheet 30

Pythagorean Theorem Worksheet 31

Pythagorean Theorem Worksheet 32

Pythagorean Theorem Worksheet 33

Pythagorean Theorem Worksheet 34

Pythagorean Theorem Worksheet 35

Pythagorean Theorem Worksheet 36

Pythagorean Theorem Worksheet 37

Pythagorean Theorem Worksheet 38

Pythagorean Theorem Worksheet 39

Pythagorean Theorem Worksheet 40

Pythagorean Theorem Worksheet 41

Pythagorean Theorem Worksheet 42

Pythagorean Theorem Worksheet 43

Pythagorean Theorem Worksheet 44

Pythagorean Theorem Worksheet 45

Pythagorean Theorem Worksheet 46

History of Pythagorean Theorem

As do all theorems, Pythagoras theorem has its genesis tales, mostly prone to dispute. The Pythagorean theorem cuts across different cultures in the world, such as Babylonian, India, and China.

For a long time, this theorem has been associated with Pythagoras, a Greek mathematician- philosopher from c.570-500/490 BCE. However, it has been documented to be far, much older.

That early evidence of this theorem has been identified in four Babylonian tablets from c. 1900-1600 BCE. There are calculations of the square root of 2 in the tablets, which is the length of the hypotenuse of a right-angled triangle whose base and perpendicular are equal to 1.

In the tablets, there are lists of special integers such as 3,4, and 5 that satisfy the Pythagoras theorem (3² + 4 = 5²). These integers are now referred to as Pythagorean triples.

This theorem can also be seen in India’s Baudhayan Sulba-sutra, which is dated back to between 800-400 BCE. Despite the different shreds of evidence of this theorem, this theorem eventually was credited to Pythagoras.

Pythagoras was from Samos (around c. 570-495 BCE). Iamblichus (Syrian historian c. 250-330 CE) documented that Pythagoras was introduced to mathematics by Thales of Miletus and his student Anaximander.

Pythagoras journeyed to Egypt around 535 BCE to broaden his knowledge and was captured by Cambyses II of Persia during the 525 BCE invasions and taken to Babylon. While in Babylon, he learned some of the Babylonian ways in arithmetic and music. He is noted to have also travelled to India before returning to Samos.

Unsatisfied with the reception of his teaching ways, he left for Croton (current Crotone in Italy). Here he established a philosophical and religious school where most of his followers (Pythagoreans) lived and worked. Pythagoras being the master, the society worked communally on discoveries and theories.

Some of Pythagoras believes included:

• All things are numbers, and mathematics forms the basis of everything.
• Numbers have characteristics, personalities, strengths, and weaknesses.
• The world is dependent on the interaction of opposites such as male and female.
• Specific symbols have mystical significance and other beliefs.

The school operated on strict secrecy believed to have been adopted during his time in Egypt.  Pythagoreans shared ideas and intellectual findings within themselves. Of the discoveries Pythagoras was credited for:

• Sum of angles of a triangle is equal to two right angles.
• The Pythagoras theorem, as defined earlier.
• The discovery of irrational numbers.
• Definition of the regular solids such as the cube, tetrahedron, and octahedron.
• That the earth is a sphere.

Many diverse proofs and extensions of the Pythagoras theorem have been developed over the years. Euclid’s renowned “windmill” proof in Book I of elements is one of these proofs. Euclid proposed that areas of similar triangles are proportional to the squares of their corresponding sides. The semicircles used to define Hippocrates of Chios’s lunes are also examples of Pythagoras theorem extension.

It is also documented that as far as the 1^st century CE, the Chinese have already solved problems that involved finding the length of one side when given the other two sides in a right-angled triangle. Additional proofs have been given by famous figures such as the Greek mathematician Pappus of Alexandria, Leonardo da Vinci and more. 

Despite all the mysteries surrounding Pythagoras’ discoveries, he remains to be a key figure in mathematics.

Usage of Pythagorean Theorem

Nowadays, trigonometry is being used across different industries and disciplines such as surveying, technology, etc.

Some of the applications of trigonometry include:

Architecture and construction 

Architecture and construction being engineering-based disciplines, the use of trigonometry in these sectors is not something new. Architecture oversees the design of structures such as buildings, bridges, dams, etc. How then is trigonometry used in engineering? You may ask. Trigonometry is adopted mostly during the design stages of engineering, that is, to determine lengths, angles, and positions of parts of a structure such as roofs, staircases, beams, columns, etc.

As an illustration of this application, we can use the example of a bridge design and construction. Trigonometry is used to determine the distribution of forces, length of loading cables, the height of supporting towers, the angle between two, and their position when testing for bridge strength.

Laying out square angles

This principle is used to determine if corners are right-angled, for example, walls, beams, windows, doors, etc. It is also referred to as the 3-4-5 method. This method is primarily based on the Pythagoras Theorem, for it is established that for a triangle with two sides measuring 3 and 4 units of length, its hypotenuse at 90-degrees will automatically be 5 units of length (3² + 4 = 5²). During the construction of the foundation, a string can be used to form a triangle of known lengths that would ordinarily form a right angle when setting out a building’s corner walls. A builder’s square can be used to determine this as it uses the same principle.

Two-dimensional navigation 

Two-dimensional navigation is used to locate positions or points of interest on air or sea. If you have two lengths/distances, you can use the Pythagorean Theorem to find the shortest route. Once you know the distance (coordinates) of a point in either direction (north, south, east, or west), you can find a ship’s distance from that point using the Pythagorean Theorem. In air navigation, the pilot can use the planes height from the ground and its distance from the airport to determine the best time and position to begin decent.

In surveying

Surveying is a key part of planning, especially in urbanization. This necessitates the use of surveyors in construction and creating maps. Surveyors use trigonometry when carrying out division and configuration of land and calculation of the size of land and slope steepness of hills and mountains—for example, distances and heights between different points.

Also, some of the equipment, such as the clinometer, working station, etc., used to determine elevation (slope) of land employs the use of the Pythagorean Theorem. The modern gadgets calculate and produce the answer, while older ones, the surveyor, had to calculate the measurements using trigonometry.

Frequently Asked Questions

Final Thoughts

The invention of the Pythagorean Theorem is still a mystery up to date as it is evidenced to have been used by different civilizations. What we can be certain of its significance to the world as we know it. Its applications cut across disciplines and industries. The major application recorded was in engineering. Well-known structures around the world like the leaning tower of Pisa, the Roman Colosseum, the Sydney Opera House, and many more are evidence of applying the Pythagoras Theorem.

About This Article

Authored by:

Jake Adams

Academic tutoring, learning resources, SAT & ACT prep, college admissions applications

Jake Adams is an academic tutor and the owner of Simplifi EDU, an online tutoring business based in Santa Monica, California. With over 14 years of professional tutoring experience, Jake is dedicated to providing his clients with the best online tutoring experience. He offers a wide range of academic subjects from K-College, specializing in SAT & ACT prep and college admissions applications. Jake has built a network of exceptional undergraduate and graduate-level tutors from top colleges across the nation. Holding a BS in International Business and Marketing from Pepperdine University, Jake combines his educational background with his expertise to deliver effective and comprehensive tutoring services.